Introduction
Once the query planner has determined the optimal plan for executing a query, it's time to implement that plan. But before we can do that, it's important to understand the algorithms used to execute the various operations in the plan.
In this post, we will delve into external merge sort and external hashing, two algorithms that are essential for efficiently working with large amounts of data that don't fit in memory. We will also discuss how these algorithms are used in executing operations such as aggregations and joins. Understanding these algorithms and how they are used is key to effectively executing queries on a database, particularly when dealing with large amounts of data.
Sorting
Sorting is a fundamental problem in computer science that has been addressed by numerous algorithms. The most well-known and efficient algorithms for sorting are merge sort and quick sort. However, these algorithms rely on the ability to access all of the keys to be sorted in memory, which is not always possible in the context of databases. To address this, adaptations of these algorithms have been developed to work with disk-oriented systems used in databases. These adaptations, known as external sorting algorithms, allow for the efficient sorting of large datasets that may not fit entirely in memory.
External Merge Sort
External sorting algorithms follow a divide-and-conquer approach to sort large datasets that do not fit in memory. The algorithm works by dividing the records into smaller runs and sorting them individually. The sorted runs are then stored on a disk.
Phase 1 (Split): The data is split into small chunks that can fit in memory, and these chunks are sorted and written back to disk.
Phase 2 (Merge): The sorted runs are merged into larger files. This process is repeated until all of the data has been sorted and merged into a single file. The resulting file is then written back to the database.
One way to perform external sorting is to use a multi-pass approach where we divide the data into runs and merge them together. In each pass, we read a batch of B pages from the input data into memory, sort them, and write them back to disk as a new run. We then take pairs of runs from the previous pass and merge them into a new run that is twice as long as the previous ones. This process is repeated until we have a single, sorted run containing all of the data.
For example, if our data set consists of N pages and we have B buffer pages available to hold the input, the first pass would involve reading B pages at a time, sorting them, and writing them to disk as new runs. In the next pass, we would take pairs of runs from the previous pass and merge them into new runs, and so on. This process continues until we have a single, sorted run containing all of the data.
This algorithm is efficient when we have a limited number of buffer pages available, but it becomes less efficient as the number of buffer pages increases. A more general version of external sorting is known as "external merge sort" which can take advantage of a larger number of buffer pages. In external merge sort, we still divide the data into runs and merge them together, but we use a more complex merging process that can handle more than two runs at a time. This allows us to sort the data more efficiently by using a larger number of buffer pages, which can reduce the number of passes and I/O operations required.
Note: there's a huge area of optimizations in this problem (like buffer pool optimizations), for example, we can use double buffering optimization, in which we ask the buffer pool to prefetch the next run in the background while we are processing the current one.
Hashing
Hashing can be very useful for grouping and organizing data based on certain criteria. However, when it comes to disk-based databases, traditional hashing techniques may need to be modified in order to work effectively. This is because disks have slower access times compared to main memory, and therefore hashing algorithms need to be designed in a way that minimizes the number of disk I/O operations required. Some techniques that can be used to optimize hashing for disk-based databases include using larger block sizes, creating smaller hash tables, and using techniques such as bucket chaining to handle collisions. By adapting traditional hashing techniques for the specific needs of disk-based databases, we can create efficient algorithms for grouping and organizing data on disk.
External Hashing
We will do the same as we did in external sort, first step (split) is to split the records into partitions using a hash function, and put those records in the disk along with other records matching the key. In the next step (Rehash), retrieve each portion from the disk, and build a new hash table based on a second different hash function.
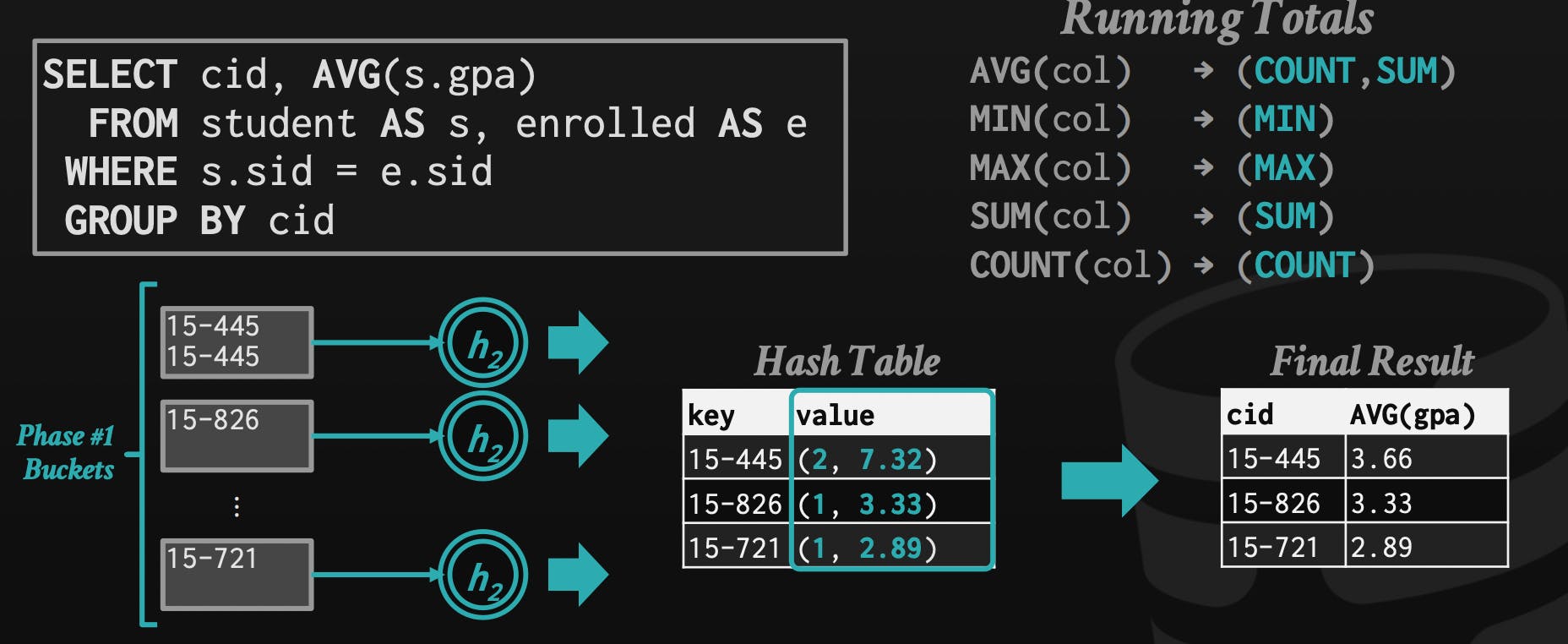
Aggregations
Aggregation operator in the query plan groups the values of one or more records into a single scalar value depending on the given query. There are two main approaches to such grouping: 1- sorting, and 2- hashing.
Aggregations using Sorting
It detects the key to group with, then sorts the records using it. If it fits in memory, then it's using quick or merge sort. However, if it doesn't fit, it will utilize external merge sorting. After that, it will perform a sequential scan on the sorted records, and compute the aggregation by looking at the occurrence of the same key.

Aggregations using Hashing
Hashing is a powerful tool to do aggregations, also, it's better to be used instead of sorting in some cases. One example is that when we don't need the results of the array sorted, so we don't need to spend too much sorting data that won't be used!
To use hashing for aggregations like AVG, MIN, MAX, SUM, and COUNT, you can simply modify the value of the hashed key to store the appropriate value for each aggregation. For example, to calculate the MIN value, you can store the minimum value seen so far at each key. To calculate the SUM, you can add the current value to the value at the key. And to calculate the AVG, you can store both the sum and the count at each key, and then divide the sum by the count to get the average.
References
CMU15-445/645 Database Systems lecture notes. Retrieved from: 15445.courses.cs.cmu.edu/fall2019
Note: ChatGPT was used to help me refine and make this post more concise, and readable, and provided some examples. So huge thanks to OpenAI!
